Curriculum links | Rubric | Student Sample
Round 1. Perambulating Squares
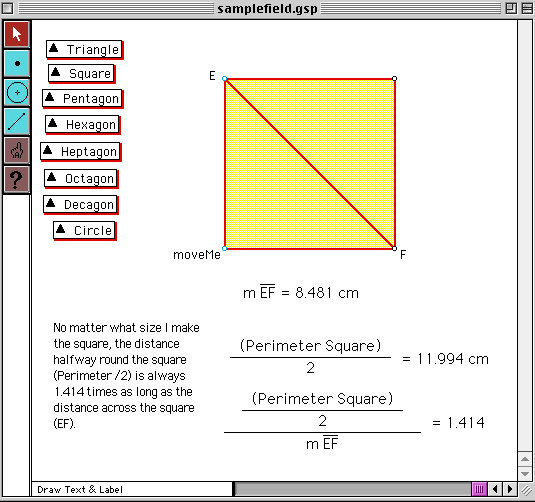
- Fran wants to visit Ed. They are as far apart on the square as they can be.
Fran can take the long way around the field to see Ed or she can cut directly across the
field.
How much farther is it to take the long way? Use the square in the sketch and The Geometer's
Sketchpad tools to help you answer this question (Download PC file
or Mac file). Explain how you solved this problem.

- How would your answer change if the square had been a different size? Drag the move Me
point to try different squares. Write your findings in a short report that uses words,
pictures, and numbers.
- Use your findings in #2 to help you answer each of these questions. Explain each of your
solutions words, drawings, and numbers.
- Q1: A field has a diagonal length of 200 m. Calculate the length of fencing needed to
enclose this field.
- Q2: A square has a perimeter of 40 cm. Calculate the length of its diagonals.
- Q3: A park takes up a whole square block. The blocks are each 250 m long. Two new
sidewalks are to be built that criss-cross the park. The town planner estimates that it will
cost about $100 per metre to build the sidewalks. Estimate total cost of the two new
sidewalks.
- Q4: Make up another square problem. Trade problems with a classmate and solve each other's
problem. Discuss each others' solutions.
Round 2. Perambulating Regular Polygons
- Pick one set of polygon questions (triangles, pentagons, hexagons, heptagons, octogons,
or decagons). Answer the first 5 questions.
- Now work with a partner, who picked a different set of questions. Carefully explain to
each other how you each solved your problems.
- Now try to answer the last two questions in your partner's problem set, Q5 and Q6.
Discuss your solutions (and see how good a teacher you each were).
Set of Triangle Questions
Q1 How much farther is it to go halfway around a equilateral triangular, compared to going
directly across it? Use the triangle in the sketch and The Geometer's Sketchpad tools to help
you answer this question.
Q2 How would your answer change if the triangle had been a different size. Drag the move Me
point to try different-sized triangles.
Use your results in Q2 to help you solve the next 3 questions
Q3 An equilateral triangle has a height of 15 cm. Calculate its perimeter.
Q4 An equilateral triangle has a perimeter of 100 m. Calculate its height.
Q5 Make up another triangle question and solve it.
Q6 (partner's question) A person took 36 paces to walk across an equilateral triangle-shaped
lawn. How many paces would it takes to walk around the lawn?
Q7 (partner's question) A person took 20 minutes to go around a walking track shaped like an
equilateral triangle. How long would it take to walk from one corner of the track directly
across to the half-way point of the track?
Set of Pentagon Questions
Q1 How much farther is it to go halfway around a regular pentagon, compared to going
directly across it? Use the pentagon in the sketch and The Geometer's Sketchpad tools to help
you answer this question.
Q2 How would your answer change if the triangle had been a different size. Drag the move Me
point to try different-sized pentagons.
Use your results in Q2 to help you solve the next 3 questions
Q3 A regular pentagon has a height of 15 cm. Calculate its perimeter.
Q4 A regular pentagon has a perimeter of 100 m. Calculate the distance shown..
Q5 Make up another regular pentagon question and solve it.
Q6 (partner's question) A person took 36 paces to walk across a regular pentagon-shaped lawn.
How many paces would it takes to walk around the lawn?
Q7 (partner's question) A person took 20 minutes to go around a walking track shaped like an
regular pentagon. How long would it take to walk from one corner of the track directly across
to the half-way point of the track?
Set of Hexagon Questions
Q1 How much farther is it to go halfway around a regular hexagon, compared to going directly
across it? Use the hexagon in the sketch and Geometer's Sketchpad tools to help you answer
this question.
Q2 How would your answer change if the hexagon had been a different size. Drag the move Me
point to try different-sized hexagons.
Use your results in Q2 to help you solve the next 3 questions
Q3 An regular hexagonÕs longest diagonals are 15 cm in length. Calculate the hexagonÕs
perimeter.
Q4 An regular hexagon has a perimeter of 100 m. Calculate the greatest distance across the
hexagon.
Q5 Make up another regular hexagon question and solve it.
Q6 (partner's question) A person took 175 paces to walk across an regular hexagon-shaped lawn.
How many paces would it takes to walk around the lawn?
Q7 (partner's question) A person took 40 minutes to go around a walking track shaped like a
regular hexagon. How long would it take to walk from one corner of the track directly across
to the half-way point of the track?
Set of Heptagon Questions
Q1 How much farther is it to go halfway around a regular heptagon, compared to going
directly across it? Use the heptagon in the sketch and Geometer's Sketchpad tools to help you
answer this question.
Q2 How would your answer change if the heptagon had been a different size. Drag the move Me
point to try different-sized heptagons.
Use your results in Q2 to help you solve the next 3 questions.
Q3 An regular heptagon has a height of 15 cm. Calculate its perimeter.
Q4 An regular heptagon has a perimeter of 100 m. Calculate its height.
Q5 Make up another heptagon question and solve it.
Q6(partner's question) A person took 120 paces to walk across an regular heptagon-shaped lawn.
How many paces would it takes to walk around the lawn?
Q7 (partner's question) A person took 15 minutes to go around a walking track shaped like an
regular heptagon. How long would it take to walk from one corner of the track directly across
to the half-way point of the track?
Set of Octagon Questions
Q1 How much farther is it to go halfway around a regular octagon, compared to going directly
across it? Use the octagon in the sketch and The Geometer's Sketchpad tools to help you answer
this question.
Q2 How would your answer change if the octagon had been a different size. Drag the move Me
point to try different-sized octagons.
Use your results in Q2 to help you solve the next 3 questions
Q3 An regular octagonÕs longest diagonals are 60 cm in length. Calculate its perimeter.
Q4 An regular octagon has a perimeter of 100 m. Calculate the length of its longest diagonal.
Q5 Make up another octagon question and solve it.
Q6 (partner's question) A person took 36 paces to walk across an equilateral triangle-shaped
lawn. How many paces would it takes to walk around the lawn?
Q7 (partner's question) A person took 20 minutes to go around a walking track shaped like an
equilateral triangle. How long would it take to walk from one corner of the track directly
across to the half-way point of the track?
Set of Decagon Questions
Q1 How much farther is it to go halfway around a regular decagon, compared to going directly
across it? Use the decagon in the sketch and The Geometer's Sketchpad tools to help you answer
this question.
Q2 How would your answer change if the decagon had been a different size. Drag the move Me
point to try different-sized decagons.
Use your results in Q2 to help you solve the next 3 questions.
Q3 An regular decagonÕs longest diagonal is 2.5 m long. Calculate its perimeter.
Q4 A regular decagon has a perimeter of 500 m. Calculate the length of its longest diagonal.
Q5 Make up another regular decagon problem and solve it.
Q6 (partner's question) A person took 36 paces to walk across an regular decagon-shaped lawn.
How many paces would it takes to walk around the lawn?
Q7 (partner's question) A person took 12 minutes to go around a walking track shaped like a
regular decagon. How long would it take to walk from one corner of the track directly across
to the half-way point of the track?
Round 3. Learning about Circular lengths
Use the circle in the Geometer's Sketchpad sketch and work out ways solving the problems below
that involve the circumference and diameter (or radius) of a circle.
Write a report on how to solve these kinds of problems. Use word, numbers, diagrams and
samples selected from the problems below in your report. Make sure you include one of your own
problem from Q7.
- A circle has a diameter of 50 cm. Calculate its circumference.
- How much fencing is needed to enclose a circular garden with a radius of 20 m?
- How far will a wheel of radius of 30 cm role in one revolution?
- The planet earth has a diameter of 12 756 km at the equator. Calculate the circumference
of the earth at the equator.
- Measure the diameter of a can. Calculate the circumference of the can. Check your
calculation by actually measuring the circumference. Write a short report on your conclusions,
using words, diagrams, and numbers.
- How much farther will a circle of diameter 100 cm role in one revolution, compared to a
circle with a circle whose diameter is 1 cm less.
- Invent a circle problem and solve it.
Overall Expectation (Gr 8, Measurement)
- Solve problems related to the calculation of the radius, diameter, and circumference of a
circle: measure the radius, diameter, and circumference of a circle using concrete material;
recognize there is a constant relationship between the radius, diameter, and circumference
of a circle and approximate its value through investigation; develop the formula for finding
the circumference of a circle; estimate and calculate the radius, diameter, and circumference
of a circle, using a formula
in a problem-solving context; define radius, diameter, and circumference and explain the
relationship between them
Teacher Notes
Note 1. Rounds 1 and 2 should establish the idea that,
- Distance halfway round regular polygon = constant (for regular polygon) X shortcut
distance, or
- Distance round regular polygon = 2 x constant (for regular polygon) X shortcut distance
Note 2. It is expected that students will adapt and apply the lessons of Rounds 1 and 2 to
calculate the circle constant in Round 3 and come up with the rule that,
- semi-circle = constant x diameter (or some equivalent rule, like, circumference = 2 x
constant x diameter)
Assessment of Performance
Level 4
- skillfully uses The Geometer's Sketchpad tools to make necessary constructions and
measurements and calculations
- clearly, concisely, and accurately identifies the relationship between semi-perimeter
(or perimeter) and 'width' of at least two regular polygons and circle
- solves most problems, few (minors) errors
- very effective at teaching partner and discussing solutions (assisting partner as
necessary)
Level 3
- proficiently uses The Geometer's Sketchpad tools to make necessary constructions
and measurements
- accurately identifies the relationship between semi-perimeter (or perimeter) and 'width'
of at least two regular polygons and circle
- successfully solves majority of proble
- has success teaching partner and discussing solutions
Level 2
- needs some assistance to effectively use The Geometer's Sketchpad tools to make
necessary constructions and measurements
- needs some assistance to identify the relationship between semi-perimeter (or perimeter)
and 'width' of at least two regular polygons and circle
- independently solves fewer than half of the problems
- has some success teaching partner, needs encouragement to participate effectively in
discussion of solutions
Level 1
- needs assistance to effectively use The Geometer's Sketchpad tools to make
necessary constructions and measurements
- needs assistance to identify the relationship between semi-perimeter (or perimeter) and
'width' of at least two regular polygons and circle
- limited success apply relationships to solve problems
- limited success in both teaching partner and discussing solutions of problems
Sample Student Response
Level 3 (Round #1)
Download PC GSP file | Download
Mac GSP file
| |