| Stories from the Classroom |
 |
Three days Sketching madly with Grade 9 students
Contributed by: David Stocks, KCVI;
Leslie Farquharson, KCVI;
Nathalie Sinclair, Queen's
The Setting: April 12th at the Computer Lab at KCVI in Kingston, Ontario. There are 24 PCs (one per student), an Overhead projector connected to a PC, and Large Blackboards. The class is just beginning a unit on geometry. We have not done any introductory work with compass and ruler constructions. This is the first time the students have seen Geometer's Sketchpad (GSP). Classes are 72 minutes per day (semestered school).
Day 1:
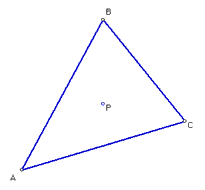
Most of the students are able to drag the vertices of the triangle intuitively to manipulate the triangles. We give them 5 minutes to manipulate the triangle shape and observe the movement of P. Given that we have four instructors available, we are easily able to move about the room and assist students experiencing difficulties. With only one teacher in the lab, it would take longer to get through the learning stages for using GSP; however, once the teacher has shown a student, this student can then show his/her neighbour and so on.
After the students have had a chance to play around with the sketch, Nathalie gathers the attention of the students and asks them what happens to the mystery point P as the vertices of the triangle are moved. Many comment that the point stays inside the triangle no matter what. One students observes that the point P seems to follow the movement of the vertex being dragged. Another student conjectures that it stays in the centre of the triangle. Nathalie asks what it means to speak of the centre of a triangle. She holds a paper triangle and asks how we would go about finding the centre of it (i.e. point P). Many call out suggestions, so many, Nathalie can't follow them all. Eventually, Zach's suggestion that she fold to find a median (of course, his terminology is not a precise) is taken up and Nathalie asks if the students can construct a median on the triangle they have in GSP. For this she must show them on the overhead how to select a segment and use the construct menu to get the midpoint, then the segment tool to draw in the median. They notice that P falls on this median. The students follow this set of instructions on their own screens. Nathalie asks where P falls along the median. Jane suggests drawing another median and the intersection is indeed at P. The third median also intersects at P. This leads into a discussion of what P might be. We introduce the idea of centre of gravity, and tell the students that the mystery point P is also called the centroid, because it is the centre of mass of a triangle. Nathalie demonstrates this with a paper triangle. We leave this concept for the time being and move on to the next sketch.
We close the file for P-triangle and open the one for the pre-made Q-triangle. There is a triangle with a mystery point Q in it. We ask the students to manipulate the vertices again. Almost immediately, oohs and aahs are audible, as Q (the orthocentre) moves much more wildly about than P did, well outside the triangle, even off the screen. After allowing them to play for a few minutes, Nathalie asks them under what conditions the point Q is inside the triangle. The first suggestion is for equilateral triangles. Nathalie asks how they could verify this. Someone suggests measuring the sides, which gives us a purposeful reason to show them how to measure lengths in GSP. We disprove the conjecture to everyone's satisfaction. The next suggestion is that it has to be a right angle triangle. This leads into measuring angles. The students observe that when there is a right angle triangle, the point Q falls on the right angle vertex of the triangle. We are still looking for the condition under which Q moves outside the triangle. Nicole suggests that there has to be an obtuse angle. This sets the students off to try looking for a triangle with non-obtuse angles that has Q outside.
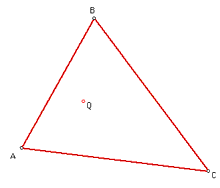
This really gets them working in a concentrated and diligent manner–the chance to show that something is impossible. It becomes clear that one angle must be obtuse for Q to be outside the triangle, but we still don't know how to construct Q.
Nathalie starts directing them towards discovering how to construct Q by questioning what sorts of lines (such as the median) they can construct and what this might indicate. She asks how they might measure the area of the triangle, which brings out the height or altitude of the triangle. After Nathalie shows them how to construct perpendicular lines, the students are quick to construct all three on their sketches and just as quickly Kevin reminds everyone they only really need two. Thus, we have developed the construction of the orthocentre. While the terms centroid and orthocentre are introduced and written on the blackboard, the students seem much more comfortable in using "point P" and "point Q" respectively when referring to these special points.
Now Nathalie asks them to construct their own mystery points, hide the constructing lines and challenge their neighbours to figure out what they are. (They turn out to be happier to challenge the instructors and watch them being stumped for a change!) Up to this point, they've just been drawing on the pre-saved sketches P and Q, so Kate naturally asks how they can construct a triangle and how they can hide lines. This is quickly shown with the overhead, as well as how to improve the appearance with different thickness lines and varying colours.
There is about half an hour left in the class and the students work keenly, constructing their own sketches. There are lots of minor technical questions about making constructions, but most are very simple for the instructors to answer. Nathalie's expertise with GSP allows her to suggest approaches for even the most difficult questions. The students are quick to experiment with angle bisectors and perpendicular bisectors, but the most interesting constructions are the mystery shapes (such as the triangle of the midpoints of the segments joining the midpoints of the initial triangle) and mystery curves (such as the arc passing through two midpoints and the foot of the altitude). Having seen that animation is possible several are soon tracing and animating very beautiful shapes. They are very proud of their mystery shapes, especially because they often have to explain to the instructors how they made them.
There is a seamless quality to this approach to teaching how to use GSP. Within an hour of seeing the program for the first time, the students are exploiting its potential to explore geometric construction and creating strikingly beautiful images. From the outset, having the pre-made sketches, allows them to begin manipulating triangles immediately and the mystery of how this is happening and whether they can control it drives them forward to discover what is possible with this tool. Thus the pre-made sketches scaffold their learning curves, igniting their curiosity. The creative aspect of the activity is striking and seems to play a large part in keeping the students motivated. It is especially satisfying to be able to combine curriculum goals with exploration and creativity. It is great to hear their repeated gasps and little outbursts about how cool, neat and other such things that kids say when they are enjoying themselves.
The process they use to create their mystery sketches is fascinating: starting from what appears to be random applications of the new constructions, they will identify something that appeals to their innate aesthetic sense, refine this or reconstruct towards it. Or else they might drag things around until an interesting shape catches their eye. One student starts using the polar co-ordinate mode to construct an incredible image that was inspired and weird. Seeing them take charge of their learning with some kind of guiding aesthetic sensibility is amazing and encouraging!
Day 2, April 13, 2000
Nathalie starts by telling the class that we will be looking at some of the mystery sketches that the students made last class. She reminds the students of what we did yesterday, mystery points P and Q, and how we used medians and altitudes to construct them. She begins by showing the students a mystery R point sketch that a few students had made in the previous class. She shows them with sketchpad how you can (instead of connecting the midpoint of one side to the opposite vertex) construct a perpendicular line to the midpoint's segment and calls this the perpendicular bisector. The students suggest that we do these constructions for all three sides of the triangle, just as we did with the constructions for finding P (the centroid) and Q (the orthomcentre). Then she leads the students through the construction of a new mystery point R (the circumcentre), showing them how to select and construct the perpendicular bisectors.
When we have point R on the overhead, she asks the students if this might be the same as point P or Q from yesterday, in order to encourage the students to think about the properties of these special points. Since R moves outside the triangle, they soon realise it can't be P. But it isn't obvious whether it is the same as Q. One student reminds the class that whenever the triangle is obtuse, the point Q is outside the triangle. So, we investigate whether this holds for our point R. It does! Nathalie asks how else we might compare the two mystery points. With some guided questioning, the students recall that the mystery point Q alsways fell on the right angle vertex of a triangle. But R falls on the opposite side rather than a vertex, so it can't be point Q. The students then suggest that in order to compare the points P, Q, and R, we can simply construct them all.
So we ask the students to start with an arbitrary triangle and construct point P, Q and R. This is a challenging activity, because they have to remember some constructions from the previous day. Many have an imprecise recollection. It is necessary for the instructors to go around and remind some of the students both what P and Q are and how we constructed them. After some students have become adept (surprisingly quickly!) they, too, go around and help out their classmates. After about 15 minutes all the students have constructed all three points on their screens.
Nathalie asks the students if they notice anything about the three points. First, someone notes that they all coincide for an equilateral triangle. Soon someone suggests they are in a straight line, but only when the triangle is isosceles. Other students disagree with this; they think the three points always form a straight line. This allows Nathalie to explore how we might connect the points and test for a straight line. Most are happy to trust to eyeballing it; one student suggests that we put a ruler on the screen to test it, but Nathalie impresses on them that this is not accurate enough for a proof. Several students want to construct a segment by selecting the three points. However, we have to point out that to construct a line, GSP can only handle 2 points. [We don't go into the Euclidean definition of a line, but this is another possible direction for the class discussion.]
We get stuck here, so Nathalie draws 3 points on the blackboard (clearly not in a line) and asks how we might prove they are not co-linear. With some more prodding, we get them to suggest that the angle formed by the three points must be 180 degrees. This gives us a good opening for showing how angles can be measured in SP. Having constructed this segment, Nathalie mentions its historical significance, that it was discovered by Euler in the 18th century and that it is one of the very special properties of triangles.
In general this is our procedure in the class. Rather than front-loading the students with information (either mathematical, or sketchpad-wise), we use exploration to open a topic and give the students a reason to want to know something. With some support from us, they are quick to learn this new application and incorporate it into their strategies for using GSP.
Nathalie now goes on to present and discuss in more detail some of the other mystery points and constructions that the students ended the previous day with. One of these is Andrew's exterior triangle vertices, constructed by making parallel lines through each vertex to the opposite sides. These three lines intersect at three points outside the triangle. When a vertex is moved, they seem to follow each other around. Andrew had traced these three points and then animated the movement of one vertex around a circle. This produced a pattern of three interlocking circles which the students found beautiful.
Another student sketch was Louise's construction of a second triangle inside the first, connecting the midpoints of the first triangle. Simon had also started with this construction, but had gone on to the constructing a third triangle connecting the midpoints of the second triangle. With Louise's construction on the projector, Nathalie asks the students what they notice about the 4 triangles we now have. The students suggest that their areas are equal. Nathalie points out that though it certainly looks that way, we should really test this conjecture out. The students ask whether we can calculate the area of triangles. Nathalie shows them how to do this in GSP by constructing the triangle interior and then measuring its area. This sets up our next investigation. We ask the students how we can subdivide triangles into smaller triangles of equal area, say with 2, 3, 4, 5, 6,… smaller triangles. The students are keen to get their construction recognised and are soon calling out they've found a way. Most are variations on median constructions. One thinks the Euler line will work to bisect the area of a triangle, but with some measuring finds that it only works in a special case. Students find a number of even numbered equal area constructions.
We keep track of the equal divisions they come up with on the blackboard. Within about 10 minutes, we have 2, 4, 16, 64, 3, 6. (the last two are found just at the end after we point out that, though it seems easy to find even number ones, nobody has yet found odd number ones). Though most students experiment with iterative processes of finding equal triangles, a few are interested in trying to find different looking triangles that still have the same area. We leave them with the quest for finding other odd number of equal area triangles.
Day 3: April 14th
We start the class by telling the students that this is going to be a lab day where they will work their own investigations and create their own sketches using some of the tools and discoveries that we have made during the past two classes. They are expected to hand them in at the end of class. Nathalie suggests 6 possible topics of investigation in order to give them an idea of what investigations are possible based on our work around triangles. We project these on the overhead and talk briefly about each one.
Sketchpad Projects
1. Make a mystery Point or Mystery Shape sketch that uses some of the properties that we investigated in class.
2. Design a balloon or a carnival ride that has a seat or bucket with a triangular shape and that needs to be held by its centroid.
3. Find out all the ways that you can divide a triangle into equal parts.
4. The Sierpinski triangle is constructed by starting with a triangle then taking out its middle triangle (the triangle whose vertices are the midpoints of the original triangle's sides), then repeating this process for each new triangle that is formed. Investigate.
5. Construct the orthocentre (our Mystery Q Point) of a triangle. Hide the altitudes that you made. Now connect the orthocentre to each of the vertices of the triangle. Three new triangles are formed. Construct the orthocentre of these three new triangles. What do you notice?
6. Which point makes the sum of the distances to each vertex a minimum? What if you started with a quadrilateral?
In order to give the students a sense of what a project would look like, since we want the students to investigate, create and also write about their work, Nathalie shows them a sample project that she has made investigating the medians of a triangle. (See image below.) The sample project shows the sketch as well as accompanying text describing the investigation and the results. It also exemplifies the extension and application of the median concept we worked with in class.
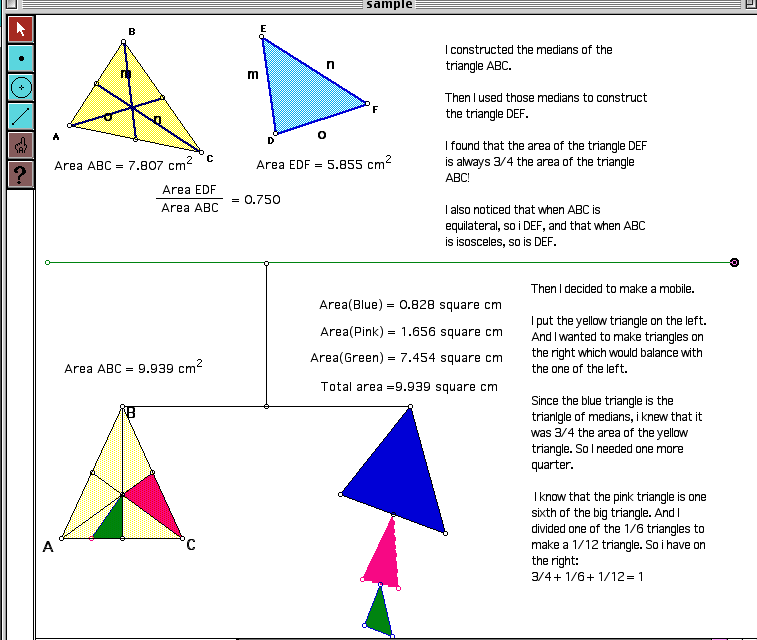
The students begin to work on their projects. We had anticipated that the students would not know how to begin, or would run out of things to investigate. This is not the case; in fact, all the students work for the entire hour. They are very meticulous in arranging their colours, labels, text, and positioning. The students ask for guidance in both using sketchpad (animating, writing text, transforming, etc.) and in identifying some of the mathematical properties of their sketches. Jordan ends up having to reverse engineer his entire sketch, trying different constructions in order to replicate the behaviour of his sketch. Though past experience has shown most students are reluctant to "write-up" their investigations, they are don't seem to mind doing it in this exercise perhaps because they get to write right beside the sketch. They can refer to their own colours and points, go back to check on their sketch how they had constructed something as they are trying to describe it, and go back and change things on the sketch as they have new ideas.
At the end of the class the students save their sketches to disk (this can be done to a server if the computers are networked or to floppy, as we did). Almost everyone has completed the assignment by the end of the allotted time. The last few are finished within 5 minutes of the end of class. The instructors can examine the sketches on GSP without needing to print them out. Some of these sketches are available in the Gallery.