Contributed by Peter Harrison
| Quadratic and Cubic Equations using Geometric models Contributed by Peter Harrison |

|
In the new courses MCR3U (Functions and Relations) and MGA4U (Geometry and Discrete Mathematics), students will be expected - among other things - to develop some fairly sophisticated understandings of conic sections and proof. This article offers some suggestions about how these topics might be delivered by developing a sequence of connected ideas that provide many opportunities for students to verify and prove mathematical results. As students are guided through the following narrative they can be asked to complete the missing details. This would be a nice break from the more familiar - explain - do examples - assign homework - cycle. All of these ideas come from René Descartes and Omar Khayyam - and no doubt many others of whom I am unaware. The fact that this is all classical mathematics, developed many years ago, does not limit its value. In fact, by examining the ideas of Descartes and Khayyam using the Geometer's Sketchpad and modern algebraic notations and techniques, students can see how beautiful mathematical ideas have woven their way down through the ages. Creative mathematics has a timeless quality and aesthetic that we often talk about but rarely share with our students. We will solve quadratic and cubic equations using geometric models. This approach has a very rich history and over time has delivered the strategies and techniques that are familiar to us today. Mathematicians had to struggle long and hard to arrive at today's conventions. By studying these ideas from geometry and algebra, students can see how much of modern mathematics was created. First, let us examine how Descartes modelled the equation y2 + ay = b2. To do this we will need to review one of the properties of a circle. In this sketch, we note that AD*AB = AE*AC . This result can be obtained by looking at the similar triangles AEB and ADC. What happens to this equation as E and C mover closer together? Download Fig1.gsp In the following diagram if we let PM = y, OP = a, and LM = b, we get the equation y2 + ay = b2. Download Fig2.gsp If we created this model using Geometer's Sketchpad, the lengths LM and LN could be altered to obtain different values for a and b. The length y, is the root of the resulting equation. You will notice that Descartes didn't mention a negative root, as this didn't have any "geometric" meaning. Also, you should note that the coefficients of our equation have to be positive. If we allow for only positive coefficients and roots, we see that there are actually three different quadratic equations that have to be solved. y2 + ay = b2, y2 = ay + b2 and y2 + b2 = ay. Descartes modelled the second of these equations by reassigning the variables to the above diagram. He let OM = y, OP = a, and LM = b. The third equation required a new diagram altogether. The following "modern" model will "solve" all quadratic equations, giving all real roots. As you can see, the following sketch has been drawn on the Cartesian plane. P is a variable point on the x-axis and Q is a variable point on the y-axis. C is at (0,1) and O is the mid-point of CF. 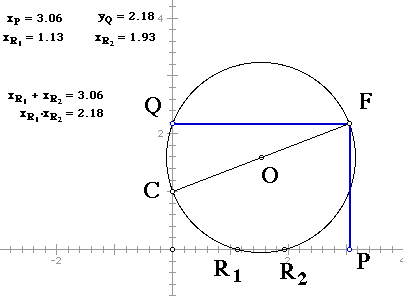
Download Fig3.gsp Let the points P, Q, R1 and R2 be (p, 0), (0, q), (r1, 0), and (r2, 0).
In order to solve cubic equations both Descartes and Khayyam showed how it is possible to reduce all such equations to one of three types. The following indicates how they accomplished this using modern algebraic notation. First, rewrite the equation 0 = X3 + aX2 + bX + C in the form 0 = x3 + dx + e by substituting x - a/3 for X. Why does this work? This equation can always be written using only positive coefficients; i.e., x3 + dx = e, x3 = dx + e and x3 + e = dx. (Note: if we are to consider only positive roots, the equation 0 = x3 + dx + e won't have any solution!) Each of these forms of the cubic equation can be solved geometrically. But first, we have to create a parabola and a hyperbola to certain specifications. To draw a parabola, Descartes used a decidedly "non-classical" approach. In the accompanying geometric model shown in the sketch, AB and BC have been constructed with varying lengths. The point C has been constructed on a hidden ray A through B. AC is a diameter of a circle. BD has been constructed perpendicular to AC. What is the relationship amongst AB, BD and BC? 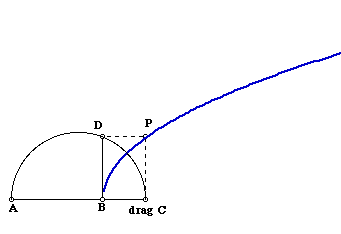
Download Fig4.gsp DP and CP have been constructed perpendicular to BD and BC respectively. The parabola is the locus of P with C as the handle. If we let the length of AB be a, the length of PC be y, the length of BC be x and place the origin at B, then the parabola will have the equation y2 = ax. Students should be asked to prove this. By altering the length of a, we can create a parabola of any shape. To solve the equation x3 + dx = e, Khayyam used the following construction. 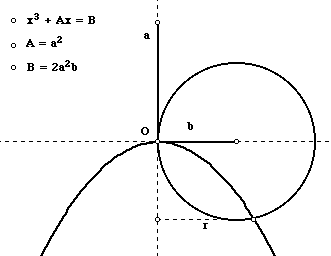
Download Fig5.gsp Here, O is the origin. The circle has been created with radius b units, centered at (b, 0). By altering the lengths of a and b, we can adjust the equation x3 + dx = e. The length r is the root of the equation. Students should verify this result by exploring the model and corresponding algebra. To solve the other two types of cubic equations, it is first necessary to construct a hyperbola. Again, the construction may seem a little unorthodox. A and C are variable points on the horizontal axis. B is fixed at the origin. b is the variable length of FB and FA. Q is at the intersection of a circle with centre F and radius FC and a perpendicular drawn to AB at B. TC is equal in length to BC. The rectangle ACTG has the same area as the square PCEN. This is a complicated construction that is very interesting to create and explore. Download Fig6.gsp The locus of point E with C as the handle is the "square" hyperbola with the equation (x+b)2/b2 - y2/b2 = 1. As the point A is moved, changing b, the hyperbola assumes different sizes with (-2b, 0) and (0, 0) as vertices. If you try to find the intersection of the hyperbola (x+b)2/b2 - y2/b2 = 1 and the parabola x2 = -ay, you will arrive at an equation in the form x3 = dx + e. Thus, the equation x3 = dx + e can be solved using the following geometric model involving both a parabola and a hyperbola. The x coordinate of the point P is the root. It should be noted that this model actually supplies all and any real roots to the equation. 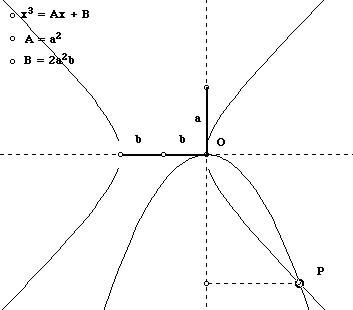
Download Fig7.gsp Some things to do and think about:
|